Notação vetorial unitária | Vetores e espaços | Álgebra Linear | Khan Academy
Quando eles estão explicando a dimensão W, ela é representada como o lado negativo do eixo X. Por que a dimensão W é negativa X? Não é realmente uma dimensão própria?

- Tente desenhar um gráfico de 4 dimensões em uma superfície de 2 dimensões. Isso é o que eles descobriram (você está certo, embora não seja um grande gráfico).
Como @NendoTaka mencionou, é muito difícil desenhar um objeto 4d em uma superfície 2d.
Veja como funciona a dimensionalidade:
com uma única dimensão, um ponto é enviado infinitamente, criando uma linha (ver X)
em 2d, adicionamos uma dimensão perpendicular a isso (ver X, Y).
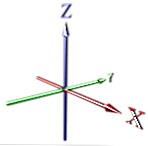
Então, vamos perpendicularmente novamente e expandimos para cima para obter a terceira dimensão (ver X, Y, Z).
Como 3d> 2d, não podemos representar tão bem no papel sem dobrar o papel ou adicionar mais folhas por cima - tudo realmente impraticável para visualização em uma tela. Então, em vez disso, usamos a perspectiva - como nossos olhos percebem 3D. Normalmente, os ângulos aqui são de aproximadamente 30 graus.

E isso parece muito bom, porque nossos olhos não veem neste sentido 3D tradicional, então imitar isso funciona. Mas, quando queremos representar uma 4ª dimensão, não temos nada para comparar. Precisamos ficar perpendiculares de novo e isso é difícil para nossos olhos compreenderem, pois não temos muita referência.
Aqui está um exemplo de representação de uma 4ª dimensão:
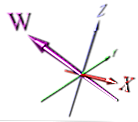
Esta é uma maneira mais correta de exibir a dimensão, mas ainda depende da perspectiva - também não é imediatamente óbvio que é uma nova dimensão à primeira vista.
Os animadores provavelmente escolheram fazer algo simples que fosse mais fácil de animar. Embora, se você girar a imagem acima, as dimensões X e W podem se sobrepor - e isso não seria óbvio na imagem sem ponteiros de seta.
Sim, eles estão errados - mas também não há uma maneira simples de representar 4 dimensões em uma única folha de papel
Fontes de imagens coordenadas e uma boa leitura
3- 1 Para ser justo, existem muitas maneiras padrão de projetar objetos 4-dimensionais como tesseratos e 3-esferas em 3 dimensões (e então até 2 dimensões nas formas usuais) que são muito superiores ao usado no show, muitos dos quais tem o bônus adicional de parecer mais legal do que o usado no show.
- @senshin oh com certeza, mas acho que os animadores também queriam explicar algo, ao invés de surpreender
- 1 Você poderia usar outras coisas além de posição para indicar a que distância de um eixo algo está, como a cor.







